Reaktionsgeschwindigkeit im Bezug auf die Konzentration

Question

Ich konnte meine letzte Frage nicht korrigieren, deswegen stelle ich sie hier nochmal korrigiert.

Aufgabe:

Gegeben sei folgende Reaktion:

A + B -> C; es gilt das Geschwindigkeitsgesetzt: v=k * c(A)

Skizzieren Sie ein Konzentrations-Zeit-Diagramm für die Konzentrationen der Stoffe A und C (-> cA = f(t) und -> cC = f(t)).

Wie verändern sich die Kurvenverläufe, wenn:

- Konzentration von A verdoppelt
- Konzentration von B verdoppelt
- Konzentration von A + B verdoppelt

Danke

Answer 1

Grüße chemweazle,

Abhängigkeit der Reaktionsgeschwindigkeit von der Konzentration

Aufgabe:

Könnte mir jemand die Konzenrations-Zeit-Diagramme für alle 3 Fälle abbilden (1.Konzentration von A wird verdoppelt, 2.Konzentration von B wird verdoppelt, 3.Konzentration von A und B wird verdoppelt)?

Verständlicher:

Ich verstehe wie sich die Reaktionsgeschwindigkeit im Fall A -> B verhält.

Aber wie verhält sich die Reaktionsgeschwindigkeit bei A + B -> C ? Nun habe ich nicht 1 Edukt und 1 Produkt im Diagramm abzubilden, sondern 2 Edukte und 1 Produkt.

Kommentar: Wie verhält sich z.B. der Kurvenverlauf, wenn: Konzentration von A verdoppelt, Konzentration von B verdoppelt, Konzentration von A + B verdoppelt

Reaktionsgleichung

A + B → C

Geschwindigkeits-Zeitgesetz: 1. Ordnung bezüglich der Ausgangstoff-Komponente A und Nullter Ordnung bezüglich des Eduktes B.

D. h. Die Reaktionsgeschwindigkeit hängt nicht von der Konzentration B, c(B), ab.

$$v(t) = k\cdot c(A)(t)$$

c(A)(t) : Momentankonzentration und v(t): Momentan-Reaktionsgeschwindigkeit
Eine Verdoplung der Konzentration von A, führt zu einer Verdopplung der Momentangeschwindigkeit.
Eine Verdopplung der Konzentration von B, unter Beibehaltung der Konzentration von A führt somit zu keiner Änderung der Reaktionsgeschwindigkeit.
Bei einer Verdopplung beider Ausgangskonzentrationen der beiden Ausgangsstoffe, A und B, führt somit nur zur einer Verdopplung der Reaktionsgeschwindigkeit, denn die Verdopplung der Ausgangskonzentration vom Edukt B erhöht die Reaktionsgeschwindigkeit nicht.
Die Reaktionsgeschwindigkeit ist ja von der Konzentration von B, c(B), unabhängig.

Zur Frage: " Wie kann man die Reaktionsgeschwindigkeit, v(t), noch ausdrücken? "

Das Produkt C und der Ausgangsstoff A haben den gleichen stöchiometrischen Koeffizienten von 1.

Reaktionsgleichung: 1 A + 1 B → 1 C

Eine Zunahme der Produktkonzentration von C führt zur betragsgleichen Konzentrationsabnahme von A, aber nur differenziell klein betrachtet.
dc(C) = - dc(A)
$$v(t) = \frac{d(C)}{dt} = - \frac{dc(A)}{dt}$$
Also:
$$v(t) = - \frac{dc(A)}{dt} = k\cdot c(A)(t)$$

Diese Differentialgleichung führt zu einer Exponential-Abkling-Funktion vom Typ: e^-k*t

Trennung der Variablen:
$$\frac{dc(A)}{c(A)(t)} = - k\cdot dt$$

Integration und die Betrachtung der Anfangsbedingung

Zum Zeitpunkt t = 0, liegt die Startkonzententration c0(A) vor. Diese nimmt im weiteren Verlauf ab zu gunsten von P. Am Anfang ist die Konzentration von C gleich Null, dafür ist die Konzentration von A noch maximal, c0(C) = 0 und c0(A) maximal.

Zum Zeitpunkt t =t liegt hat sich die Konzentration von A, c(A)(t) verkleinert und die Konzentration von C, C(C)(t) ist vom Anfangswert Null auf den Wert c(C)(t) angestiegen.

$$I = \int_{c0(A)}^{c(A)(t)} \frac{1}{c(A)(t)}\cdot dc(A(t)) = - k\cdot \int_{t=0}^{t} 1\cdot dt$$

mit

$$\int \frac{1}{x}\cdot dx = ln(x) + c$$
$$\Rightarrow für I$$
$$I = ln(cA(t)) - ln(c0(A)) = - k\cdot (t - 0)$$
$$I = ln\left(\frac{cA(t)}{c0(A)}\right) = - k\cdot t$$

Beide Seiten der Gleichung in den Exponenten der Potenz von e^{( ... )} erhoben

$$\frac{cA(t)}{c0(A)} = e^{-k\cdot t}$$

und c(A)(t):

c(A)(t) = c0(A) * e^{-k * t}

Zum Zeitpunkt t ist die Konzentration vom Anfangswert,c0(A), exponentiell auf den Momentanwert von c(A)(t) abgesunken.
Die Differenz der Konzentrationen, c0(A) - c(A)(t), ist dann der Konzentrationszuwachs an Produkt C.

c(C)(t) = c0(A) - c(A)(t) = c0(A) - c0(A) * e^{(- kt )}

Also gilt für die Konzentrations-Zeit-Abhängigkeit für das Produkt C:

C(t) = c0(A) * ( 1 - e^{- k t} )

Skizze

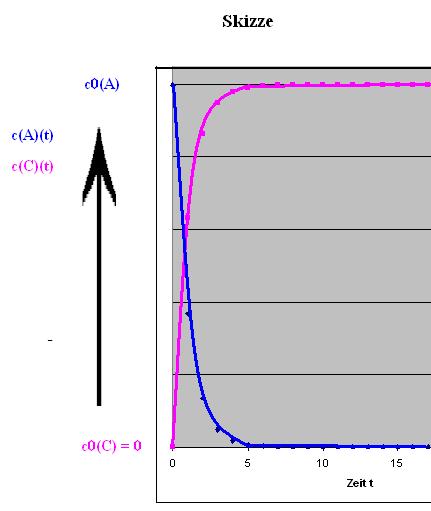
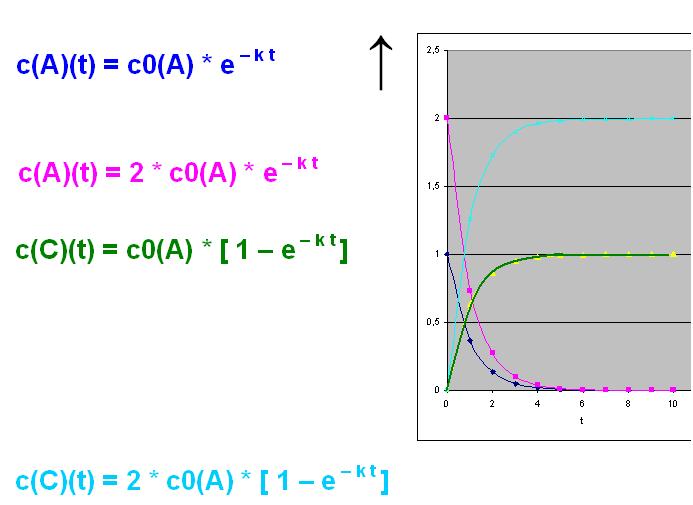
Bei der Verdopplung von der Konzentration A gilt dann für c(A)(t) und c(C)(t):

c(A)(t) = c0(A) * 2 * e^{- k t}

c(C)(t) = c0(A) * 2 * [ 1 - e^{- k t} ]

Skizze