Hallo liebe Leute,
kann mir einer bei dieser Aufgabe helfen?
In einer wüssrigen Lüsung befindet sich eine Mischung aus Kaliumiodid ( \( K I, c_{0}(K I)=0.05 \frac{\text { mol }}{L} \) ) und Chlor \( \left(C l_{2}, c_{0}\left(C l_{2}\right)=0.03 \frac{\mathrm{mol}}{\mathrm{L}}\right) \). Diese beiden Chemikalien reagieren gemäß der Reaktionsgleichung \right.
$$ 2 K I+C l_{2} \rightarrow I_{2}+2 K^{+}+2 C l^{-} $$
Die Reaktion verlaufe bei Zimmertemperatur \( \left(\vartheta=25^{\circ} \mathrm{C}\right) \) gemäß einem Geschwindigkeitsgesetz dritter Ordnung mit dem Geschwindigkeitskoeffizienten \( k=7.5 \cdot 10^{-1} \frac{\mathrm{L}^{2}}{\mathrm{mol}^{2} \cdot \mathrm{s}} \)
(a) Stellen Sie das Geschwindigkeitsgesetz gemäß der Reaktionsgleichung auf.
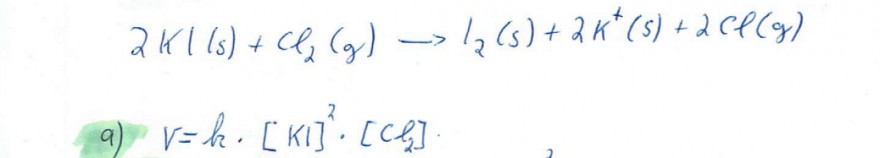
Text erkannt:
\( \quad 2 K(1 s)+C l_{2}(g) \rightarrow l_{2}(s)+2 K^{+}(s)+2 C P(g) \)
a) \( V=l_{2} \cdot[K I]^{2} \cdot\left[C l_{2}\right] \)
(b) Berechnen Sie die Anfangsreaktionsgeschwindigkeit \( v_{0} \) in dieser Lösung gemäß dem Geschwindigkeitsgesetz.
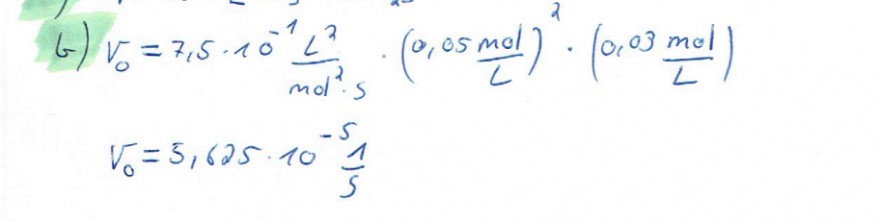
Text erkannt:
G) \( V_{0}=7,5 \cdot 10^{-1} \frac{L^{3}}{m d^{2}} \cdot S_{S} \cdot\left(0,05 \frac{\mathrm{mol}}{L}\right)^{1} \cdot\left(0,03 \frac{\mathrm{mol}}{L}\right) \)
\( V_{0}=5,625 \cdot 10^{-5} \frac{1}{5} \)
(c) Geben Sie mit Begründung an, welches der Edukte am Ende der Reaktion noch vorliegen und welches verbraucht sein wird.
Hier habe ich keine Ahnung
(d) Berechnen Sie die Reaktionsdauer unter Annahme, dass die Reaktionsgeschwindigkeit konstant bleiben würde \( \left(v=v_{0}\right) \)
Hier habe ich auch keine Ahung
(e) Nehmen Sie an, die Reaktion gehorche der RGT Regel. Mit welcher Geschwindigkeit würde die Reaktion bei \( T=340 \mathrm{K} \) ablaufen?
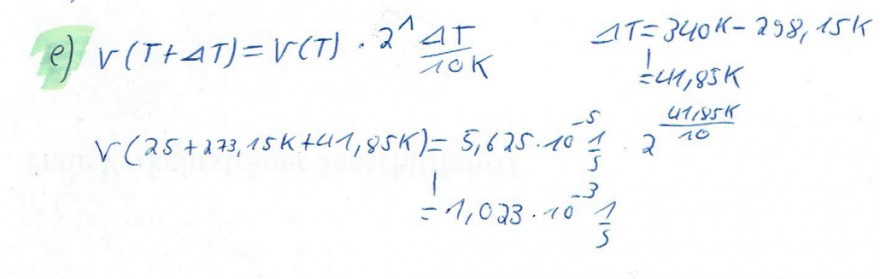
Text erkannt:
e) \( V(T+\Delta T)=V(T) \cdot 2^{1} \frac{\Delta T}{10 K} \quad \begin{array}{l}\Delta T=340^{K}-298,15 K \\ =1 \\ =41,85 K\end{array} \)
\( V(25+273,15 k+41,95 K)=5,625 \cdot 10 \frac{1}{5} \cdot 2^{\frac{41,55 k}{10}} \)
\( =1,023 \cdot 10^{-3} \frac{1}{5} \)