Hi, hier chemweazle,
NO2 + O3 → NO3 + O2
a). und b). Stimmen,- super gemacht
Anhand der Einheit der Geschwindigkeitsproportionalitätskonstanten mit:
$$\left[\frac{l}{mol\cdot s}\right],$$
läßt sich ersehen, daß ein Geschwindigkeitsgesetz 2ter Ordnung vorliegt.
Damit als Einheit für die Rate, Reaktionsgeschwindigkeitsmaß auch Reaktionsvariable genannt, mol pro liter pro sec. herauskommt, muß man mit mol2 mal l2 multiplizieren.
Ordnung n = 2
$$a). v(t) = k_{25}\cdot [NO_{2}]_{t}\cdot [O_{3}]_{t}$$
Momentanreaktionsgeschwindigkeit: v(t)
Momentankonzentrationen:
$$[NO_{2}]_{t}, [O_{3}]_{t}$$
Der Index 25 bei der Geschwindigkeitsproportionalitätskonstanten gibt die Temperatur in Celsius an.
c).Anfangsgeschwindigkeit bei t=0, v(0), bei Raumtemperatur θ = 25°C, entsprechend 298 K
$$v(0) = v_{max} = k_{25}\cdot [NO_{2}]_{0}\cdot [O_{3}]_{0}$$
$$v(0) = 4,62\cdot 10^{4} 1,6\cdot 10^{-6}\cdot 2,0\cdot 10^{-6}\cdot \dfrac{l\cdot mol^{2}}{mol\cdot l^{2}}$$
$$v(0) = 4,62\cdot 3,2\cdot 10{-8} \cdot \frac{mol}{l\cdot s} = 1,478 \cdot 10^{-7}\cdot \frac{mol}{l\cdot s}$$
d). Unter d. Annahme v(t) sei v(0) und bliebe konstant.
Die Reaktion würde so lange dauern, bis alles an Stickstoffmonoxid verbraucht wäre.
Die Konzentration von Stickstoffmonoxid ist hier in diesem Beispiel kleiner, als die Ozonkonzentration.
[NO2]0 < [O3]0
$$0 = [NO_{2}]_{0} – v(0)\cdot t$$
$$t = \dfrac{[NO_{2}]_{0}}{v(0)}$$
$$t = \dfrac{1,6\cdot 10^{-6 + 7}\cdot mol\cdot l\cdot s}{1,478\cdot mol\cdot l}$$
t = (16 / 1,478) s = 10,825 s, gerundet 11 s
e). ist super gemacht
f).Berechnung der Anfangsgeschwindigkeit v(0) bei der Temperatur von θ = 10°C, entsprechend T1 = 283 K, bzw. Umrechnung von Raumtemperatur, T2, zu der jetzt gegebenen, niedrigeren Temperatur T1
v(0)(298 K) = 1,478 * 10 -7 mol * l-1* s-1
T2 = 298 K, T1 = 283 K
$$\dfrac{k(T_{2})}{k(T_{1})} = \dfrac{k(T_{2})\cdot [NO_{2}]_{0}\cdot [O_{3}]_{0}}{k(T_{1})\cdot [NO_{2}]_{0}\cdot [O_{3}]_{0}} = \frac{v_{0}(T_{2})}{v_{0}(T_{1})}$$
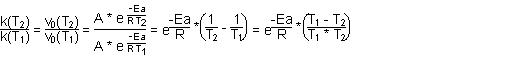
mit:
T1 - T2 = - 15 K, T1 < T2
$$\dfrac{T_{1} – T_{2}}{T_{1}\cdot T_{2}} = \dfrac{- 15\cdot K}{298\cdot 283\cdot K^{2}} = - 1,779\cdot 10{-4}\cdot K^{-1}$$
$$\frac{ - Ea}{R} = \frac{ -20,37\cdot KJ\cdot K\cdot mol}{8,314\cdot J\cdot mol} = -2450,084 K$$
$$\frac{ - Ea}{R}\cdot \dfrac{(T_{1} – T_{2})}{T_{1}\cdot T_{2}} = -2450,084 K\cdot - 1,779\cdot 10{-4}\cdot K^{-1} = + 0,436$$
$$e^{+ 0,436} = 1,547$$
$$k(283 K) = \dfrac{k(298 K)}{e^{+ 0,2906}} = \dfrac{k(298 K)}{1,547}$$
$$k(283 K) = \dfrac{46200\cdot l}{1,547\cdot mol\cdot s}$$
$$k(283 K) = 29.864,25 \frac{l}{mol\cdot s}$$
$$v_{0}(283 K) = \frac{ v_{0}(298 K)}{1,547} = \frac{1,478}{1,547}\cdot 10^{-7}\cdot \frac{mol}{l\cdot s}$$
$$v_{0}(283 K) = 9,554\cdot 10^{-8}\cdot \frac{mol}{l\cdot s}$$